Puntos, rectas y planos - Recursos educ.ar. Ana Paula Guzman
 | Autores: Miguel Serrano y Javier PeñaResponsable disciplinar: Sebastián VeraÁrea disciplinar: MatemáticaTemática: Puntos, rectas y planosNivel: Secundario, ciclo básicoSecuencia didáctica elaborada porEduc.ar |
|---|
Propósitos generales
Promover el uso de los equipos portátiles en el proceso de enseñanza y aprendizaje.
Promover el trabajo en red y colaborativo, la discusión y el intercambio entre pares, la realización en conjunto de la propuesta, la autonomía de los alumnos y el rol del docente como orientador y facilitador del trabajo.
Estimular la búsqueda y selección crítica de información proveniente de diferentes soportes, la evaluación y validación, el procesamiento, la jerarquización, la crítica y la interpretación.
Introducción a las actividades
En esta secuencia trabajaremos los conceptos de punto, recta y plano e introduciremos el concepto de recta paralela y perpendicular.
Objetivo de las actividades
- Reconocer a la geometría como parte de la condición humana.
- Saber diferenciar los distintos conceptos geométricos.
- Interpretar y reconocer figuras en el plano.
Objetivos pedagógicos
Actividad 1
La geometría se basa en tres conceptos fundamentales, el punto, la recta y el plano, que formanparte del espacio geométrico, es decir del conjunto formado por todos los puntos.
1) Miren los siguientes videos en los cuales se definen estos conceptos:
2) Respondan las siguientes consignas:
a) ¿Con qué tipo de letra suele utilizarse para denominar un plano? Recuerden que es simplemente una convención.
b) ¿Cuál es el nombre de esta letra griega: 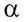 ?
?
c) ¿Cómo se llama este tipo de recta?
d)¿Qué nombre se le da a esta semirrecta?
e) En geometría punto y recta son dos términos primitivos, ¿cuál es el otro?
Actividad 2
Reunidos en grupos de dos o tres alumnos respondan las preguntas que se presentan a continuación. Utilicen lápiz, papel, regla y escuadra para corroborar sus afirmaciones. Luego verifiquen sus respuestas visitando la siguiente web.
a) ¿Cuántos puntos tiene una recta?
b) ¿Cuántas rectas contiene un plano?
c) ¿Cuántas rectas pasan por un punto? ¿Y por dos puntos? ¿Y por tres? Dibujen cada situación.
d) ¿Cuántos planos pueden intersectar a una recta en un punto?
e) ¿Es posible que dos planos se intersecten en un punto solamente?
f) ¿Pueden dos planos contener a la misma recta?
g) ¿Pueden tres planos coincidir en un punto solamente?
h) ¿Cuántos planos se pueden trazar por dos puntos distintos?
Actividad 3
1) Utilizando el programa graficador Geogebra, realicen las siguientes consignas:
a) Marquen un punto en el plano y tracen diez rectas que pasen por ese punto.
b) Utilicen la opción: Segmento dados punto extremo y longitud y grafiquen tres segmentos de 5, 10 y 15 de longitud.
c) Utilicen la opción: Polígono y grafiquen cuatro planos diferentes con 3, 4, 5 y 6 puntos en la pantalla.
Actividad de cierre
1) Miren el siguiente video (hasta el minuto 2:35) sobre rectas paralelas y perpendiculares:
a) Expliquen con sus palabras qué diferencias hay entre dos rectas paralelas y dos rectas perpendiculares. Dibujen un ejemplo para cada caso.
b) Nombren ejemplos de la vida cotidiana en los que aparezcan este tipo de rectas.
2) Miren los siguientes videos sobre como trazar rectas paralelas y perpendiculares:
a) Dibujen lo que se pide en cada video y luego redacten en el procesador de textos, instalado en sus equipos portátiles, los pasos básicos para trazar rectas paralelas y perpendiculares.
b) Utilizando regla y escuadra, dibujen una recta y un punto exterior a ella y tracen la paralela que pasa por ese punto.
c) Utilizando regla y compás, dibujen una recta y marquen un punto perteneciente a esa recta. Luego tracen una recta perpendicular que pase por ese punto.
d) Tracen dos rectas paralelas y luego una perpendicular y respondan: ¿la recta perpendicular es perpendicular a las otras dos?
e) Realicen nuevamente los ítems a y b utilizando el programa Geogebra.


Comentarios